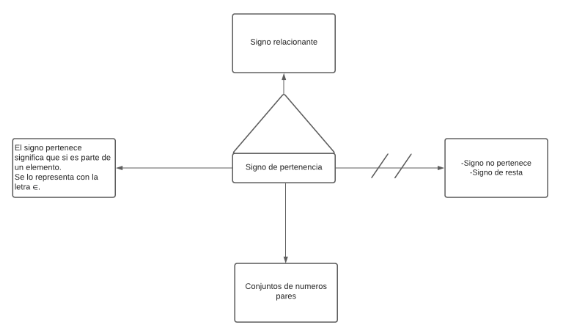
Pseudomentefacto signo pertenece
Paquete Proposicional
Supraordinada:
P1: Todo signo de pertenencia es signo relacionante.
Isoordinadas:
P2.1:Todo signo de pertenencia es el que significa que pertenece a un elemento.
P2.2:Todo signo de pertenencia se representa con el símbolo ∈.
Infraordinada:
P3: Algún signo de pertenencia es conjunto de números pares.
Exclusiones:
P4.1:Ningún signo de pertenencia es signo de no pertenece.
P4.2:Ningún signo de pertenencia es signo de resta.
Mentefactos proposicionales
P1 Todo signo de pertencia es signo relacionante.
P2.1:Todo signo de pertenencia es el que significa que pertenece a un elemento.
P2.2:Todo signo de pertenencia se representa con el símbolo ∈.
P3: Algún signo de pertenencia es conjunto de números pares.
P4: Ningún signo de pertenencia es signo de no pertenece.
P4.2:Ningún signo de pertenencia es signo de resta.
P1: Todo signo de pertenencia es signo relacionante.
P2.1:Todo signo de pertenencia es el que significa que pertenece a un elemento.
P2.2:Todo signo de pertenencia se representa con el símbolo ∈.
P3: Algún signo de pertenencia es conjunto de números pares.
P4: Ningún signo de pertenencia es signo de no pertenece.
P4.2:Ningún signo de pertenencia es signo de resta.
Argumentaciones
P1: Todo signo de pertenencia es signo relacionante.
Porque es para demostrar dónde va un elemento.
P2.1:Todo signo de pertenencia es el que significa que pertenece a un elemento.
Ya que facilita saber dónde puede ubicarse un elemento y no confundirse.
P2.2:Todo signo de pertenencia se representa con el símbolo ∈.
Porque los demás signos demuestran otro significado.
P3: Algún signo de pertenencia es conjunto de números pares.
Porque también se lo puede relacionar con otro tipo de números como los impares.
P4.1:Ningún signo de pertenencia es signo de no pertenece.
El signo de pertenencia es para saber dónde va un elemento y el signo no pertenece es para saber dónde no va un elemento.
P4.2:Ningún signo de pertenencia es signo de resta.
Porque el signo de pertenencia es un signo para mostrar dónde va un elemento y no para restarle sus dígitos.
Referencias
- Los Conjuntos: Relaciones entre conjuntos y elementos. (n.d.). GCFGlobal.org. https://edu.gcfglobal.org/es/los-conjuntos/relaciones-entre-conjuntos-y-elementos/1/
- Capítulo 1 Conjuntos, Relaciones y Funciones. 1.1. Conjuntos. 1.1.1. Conjuntos y subconjuntos, pertenencia e inclusión. Definición 1.1.1. (informal de conjunto. (n.d.). https://cms.dm.uba.ar/academico/materias/2docuat2013/algebra_I/TeoricaAlgebra201
- Noción y determinación de conjuntos (artículo). (n.d.). Khan Academy. Retrieved April 21, 2023, from. https://es.khanacademy.org/math/aritmetica-pe-pre-u/xce51e392da300f11:relaciones-logicas-y-conjuntos/xce51e392da300f11:nocion-y-determinacion-de-conjuntos/a/141-nocin-y-determinacin-de-conjuntos#:~:text=Si%20un%20elemento%20est%C3%A1%20en,%E2%88%88%2F%20para%20mostrar%20e